
정의
그래프는 노드와 노드 사이의 연결을 모은 자료구조를 말한다.
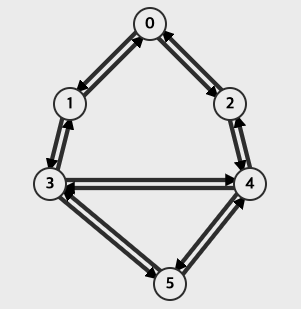
위 그래프는 양방향인 것 처럼 보이지만 양쪽 방향이 있는 것은 방향이 없는 것으로 간주한다.
용어
- vertex(정점): 노드를 말한다.
- edge: 간선
유형
- directed graph(방향 그래프): 간선에 방향이 존재한다.
- undirected graph(무방향 그래프): 간선에 존재하는 방향이 없다.
- weighted graph(가중 그래프): 간선에 부여된 값이 없다.
- unweighted graph(비가중 그래프): 간선에 부여된 값이 있다.
그래프 정렬
그래프 정렬은 간선 사이의 관계를 표현하는 방법이다.
1. 인접행렬(adjacency matrix)
- 데이터끼리 뭉쳐있고 간선이 많은 그래프에 적합
2. 인접 리스트(adjacencyList)
- 간선이 적고 퍼져있는 그래프에 적합, 인접행렬보다 더 적은 공간을 차지한다.
예시를 위한 인접 리스트 그래프를 구현해보자.
코드 및 구현

class Graph {
/**
{
0:['1', '2'],
1:['0', '3'],
2:['0', '4'],
3:['1', '4', '5'],
4:['2', '3', '5'],
5:['3', '4']
}
*/
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
// 이미 있는 정점이라면 에러처리 추가하는 것도 좋다.
if (!this.adjacencyList[vertex]) {
this.adjacencyList[vertex] = []
}
}
// 무방향 그래프는 두 정점에 모두 추가한다. 만약 방향이 있는 그래프라면 1개의 정점에만 추가한다.
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2)
this.adjacencyList[v2].push(v1)
}
removeEdge(v1, v2) {
this.adjacencyList[v1] = this.adjacencyList[v1].filter(v => v !== v2);
this.adjacencyList[v2] = this.adjacencyList[v2].filter(v => v !== v1);
}
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
const adjacentVertex = this.adjacencyList[vertex].pop();
this.removeEdge(vertex, adjacentVertex);
}
delete this.adjacencyList[vertex]
}
}
그래프 클래스는 인접 리스트로 구현하면,
객체의 key 값은 정점이고, 값은 간선 요소를 담은 배열이다.
removeVertex 메서드로 정점을 제거해줄 때는 다른 정점에 간선까지 확인해서 제거해줘야 한다.
그래프의 순회
그래프의 순회는 DFS, BFS 방법으로 가능하다.
앞서 트리 구조에서 했던 방식을 떠올려서 구현해보자.
그래프 순회의 사용
- P2P 네트워크
- 웹 크롤러
- 가장 근접한 매칭 또는 추천 찾기
- 최단 거리 문제 (GPS 네비게이션, 미로 찾기 등)
DFS - 재귀적
재귀적인 방법으로 깊이 우선 탐색을 구현해본다.
recursiveDFS(start) {
const result = [];
const visited = {};
const adjacencyList = this.adjacencyList;
(function dfs(vertex) {
if (!vertex) return null;
visited[vertex] = true;
result.push(vertex);
adjacencyList[vertex].forEach(neighbor => {
if (!visited[neighbor]) {
return dfs(neighbor);
}
})
})(start);
return result;
}
재귀 헬퍼 함수를 통해 result 값에 정점을 추가하면서 순회한다.
순서는 상관없다.
인접 리스트의 값인 간선 배열의 요소를 확인하여 visited에 존재하지 않으면
재귀 헬퍼 함수를 호출하여 가장 깊은 곳까지 도달하도록 구현했다.
결과값: ['0', '1', '3', '4', '2', '5']
DFS - 순환형
반복문을 사용하여 DFS를 구현하자.
iterativeDFS(start) {
const stack = [start];
const result = [];
const visited = {};
let currentVertex;
visited[start] = true;
while(stack.length) {
currentVertex = stack.pop();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if(!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
})
}
return result;
}
stack 구조를 활용하여 첫번째 순회를 시작하는 요소를 stack과 visited에 추가하고,
stack 구조에서 후입선출로 마지막 요소를 빼내어 해당 요소의 간선 배열을 순회하면서
visited에 존재하지 않는 요소만 stack에 push 한다.
결과값: ['0', '2', '4', '5', '3', '1']
BFS 구현
너비 우선 탐색을 queue 자료구조를 통해 구현하자.
BFS(start) {
const queue = [start];
const result = [];
const visited = {};
let currentVertex;
visited[start] = true;
while(queue.length) {
currentVertex = queue.shift();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
})
}
return result;
}
BFS 구현은 큐(Queue) 자료구조를 사용한다.
시작하는 정점을 queue와 visited에 추가하고,
queue의 첫번째 요소를 빼내어 간선 배열요소를 순회하면서
visited에 추가되지 않은 요소들만 queue에 push 한다.
시간 복잡도
|V| = 정점(노드) 갯수
|E| = 간선 갯수
| 동작 | 인접 리스트 | 인접 행렬 |
| 노드 추가 | O(1) | O(|V^2|) |
| 간선 추가 | O(1) | O(1) |
| 노드 제거 | O(|V| + |E|) | O(|V^2|) |
| 간선 제거 | O(|E|) | O(1) |
| Query | O(|V| + |E|) | O(1) |
| Storage | O(|V| + |E|) | O(|V^2|) |
참조
'Algorithm' 카테고리의 다른 글
| [Udemy] 해쉬 테이블(Hash Table)이란 ? (0) | 2024.08.09 |
|---|---|
| [Udemy] 이진 힙(Binary heap)과 우선순위 큐(Priority Queue) (0) | 2024.08.08 |
| [Udemy] Tree 순회 - BFS, DFS 이란? (0) | 2024.08.06 |
| [Udemy] 이진 검색 트리(Binary Search Tree)란? (0) | 2024.08.06 |
| [Udemy] 큐(Queue)란? (0) | 2024.08.02 |



